噪点处理
当前,在验证码图像处理中,我们一般还会进行图像滤波操作,图像滤波的目的有2个:
- 抽出对象的特征作为图像识别的特征模式;
- 为适应图像处理的要求,消除图像数字化时混入的噪声。
所以通过滤波处理来去噪,就需要我们:
- 保留图像的轮廓以及边缘等重要信息
- 使得图像清晰,视觉效果好
1. 滤波算法
目前比较经典的图像去噪算法主要有以下几种:
属于线性滤波的有:
均值滤波算法:主要思想为邻域平均法,即用几个像素灰度的平均值来代替每个像素的灰度。有效抑制加性噪声,但容易引起图像模糊,可以对其进行改进,主要避开对景物边缘的平滑处理。
均值滤波(领域平均滤波)
高斯滤波
属非线性滤波的有
中值滤波:基于排序统计理论的一种能有效抑制噪声的非线性平滑滤波信号处理技术。中值滤波的特点即是首先确定一个以某个像素为中心点的邻域,一般为方形邻域,也可以为圆形、十字形等等,然后将邻域中各像素的灰度值排序,取其中间值作为中心像素灰度的新值,这里领域被称为窗口,当窗口移动时,利用中值滤波可以对图像进行平滑处理。其算法简单,时间复杂度低,但其对点、线和尖顶多的图像不宜采用中值滤波。很容易自适应化。
双边滤波
现在我们调用 python 之中的 opencv 模块进行验证码的简单处理,代码如下:
import tesserocr
import cv2
import matplotlib.pyplot as plt
def otsu_s(img):
ret, th = cv2.threshold(img,0,255,cv2.THRESH_BINARY+cv2.THRESH_OTSU)
return ret, th
# 高斯滤波器
def guassian_blur(img, a, b):
#(a,b)为高斯核的大小,0 为标准差, 一般情况a,b = 5
blur = cv2.GaussianBlur(img,(a,b),0)
# 阈值一定要设为 0!
ret, th = otsu_s(blur)
return ret, th
# 均值滤波器
def hamogeneous_blur(img):
blur = cv2.blur(img,(5,5))
ret, th = otsu_s(blur)
return ret, th
# 中值滤波器
def median_blur(img):
blur = cv2.medianBlur(img,5)
ret, th = otsu_s(blur)
return ret, th
#双边滤波器
def bilatrial_blur(img):
blur = cv2.bilateralFilter(img,9,75,75)
ret, th = otsu_s(blur)
return ret, th
def main():
"""
测试模糊处理后otsu's二值化
:return:
"""
img = cv2.imread('test_pic.png', 0)
ret1, th1 = guassian_blur(img, 5, 5)
ret2, th2 = bilatrial_blur(img)
cv2.imwrite('temp1.png', th1)
cv2.imwrite('temp2.png', th2)
titles = ['original', 'guassian', 'bilatrial']
images = [img, th1, th2]
for i in range(3):
plt.subplot(1,3,i+1)
plt.imshow(images[i], 'gray')
plt.title(titles[i])
plt.xticks([])
plt.yticks([])
plt.show()
首先,我们来查看一下原始的验证码图片:

下面是代码运行结果:

虽然生成了结果,可是如果直接用 ocr 工具还是难以识别。毕竟大多数验证码字符本身不是标准的打印体,而且字符相对较小、图片像素较低、字符笔画较细,所以滤波算法的降噪效果不是很好。
2. 领域算法去噪
噪点往往具有孤立性。对于每个像素点,我们可以有不同的算法统计其周围D个像素点的灰度值为0或255的个数。像素 p(x,y)的D邻域(临近的像素点)就是该像素点四个顶点对于的点,坐标如下:
(x+1,y+1)、(x+1,y-1)、(x-1,y+1)、(x-1,y-1)
用ND(p)表示像素p的D邻域:

而在一幅图像中,位于坐标(x,y)处的像素p有4个相邻的像素,分别位于其上下左右,其坐标如下:
(x+1,y)、(x-1,y)、(x,y+1)、(x,y-1)
用N4(p)表示像素p的4邻域:

最后,像素p(x,y)的8邻域就是这个像素的4邻域的点+ D邻域的点;用N8(p)表示像素p的8邻域:
N8(p) = N4(p) + ND(p)
from PIL import Image
im = Image.open("test_pic.png")
im = im.convert("L") # 转换为灰度图
im = im.convert("1") # 转换为二值图
def neighbor8filter(img, p):
pixels = img.load()
w, h = img.size
# remove edges
for x in range(w):
pixels[x, 0] = 255
pixels[x, h - 1] = 255
for y in range(h):
pixels[0, y] = 255
pixels[w - 1, y] = 255
for y in range(1, h - 1):
for x in range(1, w - 1):
if not pixels[x, y]:
count = 0
for m in range(x - 1, x + 2):
for n in range(y - 1, y + 2):
if not pixels[m, n]:
count = count + 1
if count <= p:
pixels[x, y] = 255
return img
im = neighbor8filter(im, 4)
im.show()
结果:
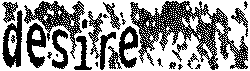
3. 连通域降噪
对于较大的噪点,还有一个思路就是求其面积,因为字符像素点大部分都是相互连通的,因此求出每一个相互连通的黑色点的个数,如果个数很多那么就说明这一片像素点很有可能是字符的部分,如果一个连通域的像素个数很少,那么基本可以确定这一片像素点就是噪点。
泛水填充法(Flood fill),就是这样的思路,从一个区域中提取若干个连通的点与其他相邻区域区分开(或分别染成不同颜色)。利用 OpenCV,我们可以方便地求出联通区域。
在计算过程中,每扫描到一个黑色的像素点,就将与该点连通的所有点的灰度值都改为同一个非零的值,因此这一个连通域的点都不会再次重复计算了。继续扫描下一个黑色像素点的所有连通点,把它们的灰度值都改为2,这样依次递增,经过上面的降噪后,验证码只剩下较大的噪点,因此验证码连通域个数不会太大,不会超过灰度值的最大范围。
直到所有的点都扫描完。接下来再次扫描所有的点,统计每一个灰度值对应的点的个数,每一个灰度值的点的个数对应该连通域的大小,并且已经包含在某个连通域上的点不会被重复计算。这样一来就统计到了每个连通域的大小,再根据预设的阀值,如果该连通域大小小于阀值,则其就为噪点。这个算法比较适合检查较大的噪点,与上面的算法正好相反。
衔接邻域算法案例,代码实例如下:
import tesserocr
import cv2
def flood_filter(img, p):
tmp_img = cv2.cvtColor(numpy.array(img.convert('RGB')), cv2.COLOR_RGB2BGR)
h, w = tmp_img.shape[:2]
mask = numpy.zeros((h + 2, w + 2), numpy.uint8)
color = 1
for x in range(w):
for y in range(h):
if (tmp_img[y, x] == 0).all():
cv2.floodFill(tmp_img, mask, (x, y), (0, 0, color))
color = color + 1
color_count = numpy.zeros(255, numpy.uint)
for x in range(h):
for y in range(w):
if (tmp_img[x, y] != 255).any():
color_count[tmp_img[x, y][2]] += 1
for x in range(h):
for y in range(w):
if (tmp_img[x, y] != 255).any() and color_count[tmp_img[x, y][2]] <= p:
tmp_img[x, y] = (255, 255, 255)
for x in range(h):
for y in range(w):
if tmp_img[x, y][2] < 255:
tmp_img[x, y] = (0, 0, 0)
return Image.fromarray(tmp_img).convert('1')
num = 20
while num > 0:
num -= 1
img = neighbor8filter(im, 4.5)
im2 = flood_filter(img,20)
im2.show()
print(tesserocr.image_to_text(im2))
识别结果为 d€§j re?”r 还需要进一步处理。